mots-clés: géométrie simplctique
L'étude des formes bilinéaires symétriques donne lieu à la géométrie euclidienne, la géométrie riemannienne,
et la géométrie pseudo-riemannienne. Au contraire, l'étude des formes
bilinéaires alternées donne lieu à la géométrie symplectique. Ce cours a
pour objectif d'introduire les principales définitions et les
propriétés élémentaires des formes symplectiques, en commençant par une
première étude en algèbre linéaire.
Rappels d'algèbre linéaire
Rappels d'algèbre linéaire réelle
Sur un espace vectoriel V, une forme bilinéaire  est dite :
est dite :
 où
où  et
et  .
.
Une forme bilinéaire a sur V induit une application linéaire définie comme suit :
définie comme suit : 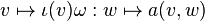 . Le noyau de la forme a désigne le noyau de cette application linéaire.
. Le noyau de la forme a désigne le noyau de cette application linéaire.
 est dite :
est dite :- symétrique lorsque pour tous vecteurs v et w de V, on a :
 ;
;
- antisymétrique lorsque pour tous vecteurs v et w de V, on a :
 .
.
 où
où  et
et  .
.Une forme bilinéaire a sur V induit une application linéaire
 définie comme suit :
définie comme suit : 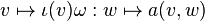 . Le noyau de la forme a désigne le noyau de cette application linéaire.
. Le noyau de la forme a désigne le noyau de cette application linéaire.Espace vectoriel symplectique
Définition
Sur un espace vectoriel réel V, une forme symplectique est une forme bilinéaire  , supposée :
, supposée :
 , supposée :
, supposée :- antisymétrique : pour tous vecteurs v et w de V,
 ;
; - non-dégénérée : pour tout vecteur v, il existe au moins un vecteur w tel que
 .
.
- antisymétrique : pour tous vecteurs v et w de V,
La non-dégénérescence signifie exactement que le noyau de ω est nul, ou encore, que ω réalise un isomorphisme linéaire  .
.
 .
.- Remarque : L'existence d'une forme symplectique implique que la dimension de V soit paire. Ce fait sera établi par la classification des formes symplectiques donnée ci-dessous.
Définition
Si  et
et  sont deux espaces vectoriels symplectiques, une application linéaire
sont deux espaces vectoriels symplectiques, une application linéaire  est dite symplectique lorsque, pour tous v et w dans V₁, on a :
est dite symplectique lorsque, pour tous v et w dans V₁, on a :
 .
.
Certains auteurs parlent de transformation canonique. Si v est un vecteur du noyau de T, v appartient a fortiori au noyau de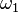 . Comme
. Comme 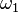 est non dégénérée, v est nul. Il s'en suit que toute transformation canonique est nécessairement injective.
est non dégénérée, v est nul. Il s'en suit que toute transformation canonique est nécessairement injective.
 et
et  sont deux espaces vectoriels symplectiques, une application linéaire
sont deux espaces vectoriels symplectiques, une application linéaire  est dite symplectique lorsque, pour tous v et w dans V₁, on a :
est dite symplectique lorsque, pour tous v et w dans V₁, on a : .
.Certains auteurs parlent de transformation canonique. Si v est un vecteur du noyau de T, v appartient a fortiori au noyau de
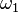 . Comme
. Comme 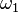 est non dégénérée, v est nul. Il s'en suit que toute transformation canonique est nécessairement injective.
est non dégénérée, v est nul. Il s'en suit que toute transformation canonique est nécessairement injective.
En particulier, les transformations canoniques d'un espace symplectique 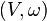 dans lui-même forment un sous-groupe du groupe
dans lui-même forment un sous-groupe du groupe 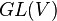 des isomorphismes linéaires de V, noté
des isomorphismes linéaires de V, noté 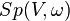 . On reviendra sur l'étude de ce groupe.
. On reviendra sur l'étude de ce groupe.
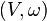 dans lui-même forment un sous-groupe du groupe
dans lui-même forment un sous-groupe du groupe 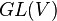 des isomorphismes linéaires de V, noté
des isomorphismes linéaires de V, noté 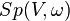 . On reviendra sur l'étude de ce groupe.
. On reviendra sur l'étude de ce groupe.
L'exemple suivant est fondamental :
Exemple 1
Les coordonnées d'un vecteur de l'espace  sont notées
sont notées  . L'espace V est muni de la forme symplectique :
. L'espace V est muni de la forme symplectique :
 .
.
La forme est représentée par la matrice antisymétrique :
est représentée par la matrice antisymétrique :
 ;
;
où In désigne la matrice identité de taille n.
 sont notées
sont notées  . L'espace V est muni de la forme symplectique :
. L'espace V est muni de la forme symplectique : .
.La forme
 est représentée par la matrice antisymétrique :
est représentée par la matrice antisymétrique : ;
;où In désigne la matrice identité de taille n.
C'est essentiellement le seul espace symplectique de dimension 2n, du
moins à isomorphisme linéaire près. Ce point est démontré dans la
section suivante. Cependant, l'isomorphisme n'est pas unique. En
pratique, la manière dont se présente un espace symplectique joue un
rôle important. D'autres exemples d'espaces symplectiques souvent
utilisés seront donnés après la classification.
Classification
Rappelons le résultat suivant :
Théorème
Soit  une forme antisymétrique sur un espace vectoriel réel E de dimension finie. On note r la dimension du noyau. Il existe une base
une forme antisymétrique sur un espace vectoriel réel E de dimension finie. On note r la dimension du noyau. Il existe une base  avec
avec  telle que :
telle que :
 une forme antisymétrique sur un espace vectoriel réel E de dimension finie. On note r la dimension du noyau. Il existe une base
une forme antisymétrique sur un espace vectoriel réel E de dimension finie. On note r la dimension du noyau. Il existe une base  avec
avec  telle que :
telle que : forme une base du noyau de a ;
forme une base du noyau de a ; ,
,  et
et  .
.
Démonstration
Procédons par récurrence sur la dimension de E.
 où
où  et
et  .
.
- Initialisation : en dimension 0, la seule forme bilinéaire sur l'espace nul est l'application nulle, la seule base est la famille vide et le résultat s'applique (avec r = 0 et k = 0).
- Supposons le résultat démontré jusqu'à la dimension n-1.
- Si a est la forme nulle, alors le noyau de a est E ; et toute base de E convient. Sinon, fixons un vecteur X₁ de E qui ne soit pas dans le noyau de a. Choississons un vecteur Y₁ tel que a(X₁,Y₁) soit non nul. Quitte à modifier Y₁ en Y₁/a(X₁,Y₁), on est en droit de supposer a(X₁,Y₁)=1. Les vecteurs X₁ et Y₁ sont non colinéaires et engendrent donc un plan vectoriel P.
-
- L'ensemble des vecteurs v vérifiant
 est un sous-espace vectoriel Q de E. Tout vecteur w peut s'écrire :
est un sous-espace vectoriel Q de E. Tout vecteur w peut s'écrire :
- L'ensemble des vecteurs v vérifiant
 où
où  et
et  .
.-
- En particulier, P et Q sont supplémentaires. Le noyau de a est évidemment contenu dans Q. Appliquons l'hypothèse de récurrence à la restriction b de a à Q. Il existe une base
 du noyau de b, étendue en une base
du noyau de b, étendue en une base  vérifiant les identités
vérifiant les identités  ,
,  et
et  .
. - La famille
 vérifie les propriétés requises. (Le noyau de a est égal au noyau de b.)
vérifie les propriétés requises. (Le noyau de a est égal au noyau de b.)
- En particulier, P et Q sont supplémentaires. Le noyau de a est évidemment contenu dans Q. Appliquons l'hypothèse de récurrence à la restriction b de a à Q. Il existe une base
Appliquons ce résultat d'algèbre linéaire réelle au cas d'une forme
symplectique ω. Comme ω est non-dégénérée, le noyau est nul (donc r =
0). Le théorème précédent donne l'existence d'une base  avec 2k la dimension de V. On en déduit que :
avec 2k la dimension de V. On en déduit que :
 avec 2k la dimension de V. On en déduit que :
avec 2k la dimension de V. On en déduit que :- La dimension d'un espace symplectique est paire.
De plus, L'application  qui à v associe ses coordonnées dans la base
qui à v associe ses coordonnées dans la base  est visiblement symplectique pour la forme symplectique usuelle
est visiblement symplectique pour la forme symplectique usuelle  sur
sur  . D'où :
. D'où :
 qui à v associe ses coordonnées dans la base
qui à v associe ses coordonnées dans la base  est visiblement symplectique pour la forme symplectique usuelle
est visiblement symplectique pour la forme symplectique usuelle  sur
sur  . D'où :
. D'où :- En dimension 2n, il n'existe à isomorphisme près qu'un unique espace vectoriel symplectique.
Exemples
Exemple 2
En géométrie symplectique, étant donné un espace vectoriel réel (de dimension finie) E, il est courant de noter les coordonnées d'un point de l'espace 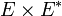 sous la forme
sous la forme  . Les dernières coordonnées p sont pensées comme l'impulsion, les premières q comme la position. L'espace
. Les dernières coordonnées p sont pensées comme l'impulsion, les premières q comme la position. L'espace 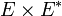 est alors muni de la forme symplectique suivante :
est alors muni de la forme symplectique suivante :  .
.
Si est un isomorphisme linéaire, alors sa transposée
est un isomorphisme linéaire, alors sa transposée  est elle-même inversible. De fait,
est elle-même inversible. De fait,  est un isomorphisme linéaire
est un isomorphisme linéaire  . Cet isomorphisme est symplectique pour les formes
. Cet isomorphisme est symplectique pour les formes  et
et  .
.
Justification : Cette forme est clairement bilinéaire et antisymétrique. Pour la non dégénérescence, prenons un vecteur non nul . Deux possibilités apparaissent :
. Deux possibilités apparaissent :
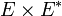 sous la forme
sous la forme  . Les dernières coordonnées p sont pensées comme l'impulsion, les premières q comme la position. L'espace
. Les dernières coordonnées p sont pensées comme l'impulsion, les premières q comme la position. L'espace 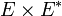 est alors muni de la forme symplectique suivante :
est alors muni de la forme symplectique suivante :  .
.Si
 est un isomorphisme linéaire, alors sa transposée
est un isomorphisme linéaire, alors sa transposée  est elle-même inversible. De fait,
est elle-même inversible. De fait,  est un isomorphisme linéaire
est un isomorphisme linéaire  . Cet isomorphisme est symplectique pour les formes
. Cet isomorphisme est symplectique pour les formes  et
et  .
.Justification : Cette forme est clairement bilinéaire et antisymétrique. Pour la non dégénérescence, prenons un vecteur non nul
 . Deux possibilités apparaissent :
. Deux possibilités apparaissent :- Soit l'impulsion p₁ est non nul : on prend p₂=0 et
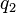 un vecteur de E qui n'est pas dans le noyau de p₁. Dans ce cas,
un vecteur de E qui n'est pas dans le noyau de p₁. Dans ce cas,  .
. - Soit l'impulsion p₁ est nulle, auquel cas q₁ est nécessairement non nul. Comme
 sépare les points de E, il existe une forme linéaire
sépare les points de E, il existe une forme linéaire  sur E vérifiant
sur E vérifiant  . En prenant
. En prenant  , on trouve
, on trouve  .
.
Exemple 3
Si (E,g) est un espace vectoriel euclidien, le dual E* s'identifie à E via l'isomorphisme linéaire  induit par la forme bilinéaire g. La forme symplectique
induit par la forme bilinéaire g. La forme symplectique  définie sur
définie sur 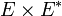 induit alors une forme symplectique sur
induit alors une forme symplectique sur  :
:  .
.
Toute isométrie induit une transformation canonique :
induit une transformation canonique : 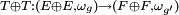 .
.
Remarque : L'exemple 1 est un cas particulier de l'exemple 3.
 induit par la forme bilinéaire g. La forme symplectique
induit par la forme bilinéaire g. La forme symplectique  définie sur
définie sur 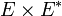 induit alors une forme symplectique sur
induit alors une forme symplectique sur  :
:  .
.Toute isométrie
 induit une transformation canonique :
induit une transformation canonique : 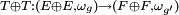 .
.Remarque : L'exemple 1 est un cas particulier de l'exemple 3.
Exemple 4
Si (H,h) est un espace vectoriel hermitien, H est naturellement muni d'une forme symplectique :
 .
.- Toute isométrie
 est symplectique pour les formes
est symplectique pour les formes  et
et  .
.
- Antisymétrie : Si v et w sont dans H, alors par sesquilinéarité,
 . En particulier, en prenant la partie imaginaire,
. En particulier, en prenant la partie imaginaire,  .
. - Non-dégénérescence : Pour un vecteur non nul v de H, on a :
 .
.
Structure complexe
En fait, tout espace vectoriel symplectique peut être obtenu comme
dans l'exemple 4. Plus exactement, toute forme symplectique sur un
espace vectoriel réel peut être vue comme la partie imaginaire d'une
forme hermitienne sur V muni d'une structure complexe.
Définition
Une structure complexe (ou structure complexe linéaire) sur un espace vectoriel réel V est la réalisation de V comme espace vectoriel complexe. Elle est déterminée par la seule action de i, donnée par un endomorphisme réel J de V vérifiant : 
Remarque : La structure complexe J est inversible et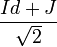 est une racine carrée de J.
est une racine carrée de J.

Remarque : La structure complexe J est inversible et
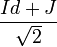 est une racine carrée de J.
est une racine carrée de J.
Alors :
Théorème
Si v est muni d'une forme symplectique ω, une structure complexe J est dite ω-compatible lorsque :
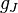 est un produit euclidien sur V ; et
est un produit euclidien sur V ; et  est un produit hermitien sur l'espace vectoriel complexe
est un produit hermitien sur l'espace vectoriel complexe  .
.
- J est un isomorphisme symplectique, ce qui équivaut à ce que
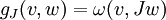 définisse une forme bilinéaire symétrique ;
définisse une forme bilinéaire symétrique ; 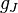 est définie positive.
est définie positive.
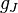 est un produit euclidien sur V ; et
est un produit euclidien sur V ; et  est un produit hermitien sur l'espace vectoriel complexe
est un produit hermitien sur l'espace vectoriel complexe  .
.
Vérifications
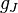 est une forme bilinéaire symétrique :
est une forme bilinéaire symétrique :
 ;
; est un produit hermitien :
est un produit hermitien :
 . On montre ainsi que
. On montre ainsi que  est sesquilinéaire. Par ailleurs,
est sesquilinéaire. Par ailleurs,  est visiblement défini positif : pour tout vecteur non nul v, on a :
est visiblement défini positif : pour tout vecteur non nul v, on a :  .
.
Théorème
Pour tout espace vectoriel symplectique 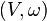 il existe une structure presque complexe ω-compatible.
il existe une structure presque complexe ω-compatible.
De plus, l'nsemble I(V) des structures complexes ω-compatibles forme une partie connexe de GL(V). Les groupes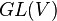 et
et 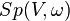 agissent transitivement sur I(V) par conjugaison.
agissent transitivement sur I(V) par conjugaison.
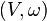 il existe une structure presque complexe ω-compatible.
il existe une structure presque complexe ω-compatible.De plus, l'nsemble I(V) des structures complexes ω-compatibles forme une partie connexe de GL(V). Les groupes
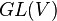 et
et 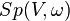 agissent transitivement sur I(V) par conjugaison.
agissent transitivement sur I(V) par conjugaison.
Démonstration
- Existence :
- Soit g un produit euclidien sur V. Il existe un unique endomorphisme g-antisymétrique A tel que, pour tous vecteur v et w :
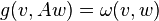 . La décomposition polaire donne : A=O.J où O est un endomorphisme orthogonal. Alors J est une structure complexe ω compatible.
. La décomposition polaire donne : A=O.J où O est un endomorphisme orthogonal. Alors J est une structure complexe ω compatible.
- Par construction, les endomorphismes J ainsi obtenus sont exactement toutes les structures complexes ω-compatibles, et dépendent continument du produit euclidien g. De fait, l'espace I(V) est l'image continue de l'espace des produits euclidiens sur V. De fait, il est connexe.
- Action par conjugaison :
- A compléter ...
Note : Dans le livre de Michèle Audin, il est rapporté un résultat de Sévennec établissant un difféomorphisme de I(V) sur un ouvert de l'espace des matrices symétriques.
Exemple 4 bis
La multiplication par i sur un espace hermitien  est une isométrie J, et donc en particulier, une structure complexe et un isomorphisme symplectique de
est une isométrie J, et donc en particulier, une structure complexe et un isomorphisme symplectique de  . On constate que la forme bilinéaire symétrique définie alors par
. On constate que la forme bilinéaire symétrique définie alors par  et
et  est
est  . En particulier, elle est non dégénérées, et donc J est
. En particulier, elle est non dégénérées, et donc J est  -compatible. La forme hermitienne h n'est autre que la forme hermitienne associée à
-compatible. La forme hermitienne h n'est autre que la forme hermitienne associée à  .
.
 est une isométrie J, et donc en particulier, une structure complexe et un isomorphisme symplectique de
est une isométrie J, et donc en particulier, une structure complexe et un isomorphisme symplectique de  . On constate que la forme bilinéaire symétrique définie alors par
. On constate que la forme bilinéaire symétrique définie alors par  et
et  est
est  . En particulier, elle est non dégénérées, et donc J est
. En particulier, elle est non dégénérées, et donc J est  -compatible. La forme hermitienne h n'est autre que la forme hermitienne associée à
-compatible. La forme hermitienne h n'est autre que la forme hermitienne associée à  .
.
Exemple 3 bis
L'espace vectoriel  est muni d'une structure presque complexe naturelle
est muni d'une structure presque complexe naturelle  . Si E est munie d'un produit euclidien g, alors J est
. Si E est munie d'un produit euclidien g, alors J est  compatible, et le produit euclidien associé est précisément
compatible, et le produit euclidien associé est précisément  .
.
 est muni d'une structure presque complexe naturelle
est muni d'une structure presque complexe naturelle  . Si E est munie d'un produit euclidien g, alors J est
. Si E est munie d'un produit euclidien g, alors J est  compatible, et le produit euclidien associé est précisément
compatible, et le produit euclidien associé est précisément  .
.Sous-espaces d'un espace symplectique
Définition
L’orthogonal d'un sous-espace W d'un espace vectoriel symplectique 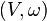 est défini par :
est défini par :
 .
.
L'orthogonal n'est pas nécessairement un sous-espace supplémentaire.
Par exemple, l'orthogonal d'une droite vectorielle la contient.
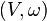 est défini par :
est défini par : .
.| Propriétés |
Pour tous sous-espaces W₁ et W₂ d'un espace symplectique 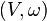 , on a : , on a :
|
On a ainsi plusieurs cas particuliers :
Définitions
Un sous-espace vectoriel W d'un espace symplectique 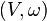 est dit :
est dit :
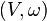 est dit :
est dit :- isotropique lorsque W est contenu dans son orthogonal ;
- lagrangien lorsque W est égal à son orthogonal ;
- coistotropique lorsque W contient son orthogonal.
L'orthogonal d'un hyperplan H est une droite D. L'orthogonal de D, à savoir H, doit contenir D. Autrement dit, l'orthogonal de H est contenu dans H : tout hyperplan est nécessairement coisotropique.
Exemple 5
Si  est un espace vectoriel symplectique, l'espace
est un espace vectoriel symplectique, l'espace 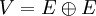 est muni de la forme symplectique
est muni de la forme symplectique  . Le graphe d'une application linéaire
. Le graphe d'une application linéaire  est un sous-espace lagrangien ssi T est symplectique.
est un sous-espace lagrangien ssi T est symplectique.
 est un espace vectoriel symplectique, l'espace
est un espace vectoriel symplectique, l'espace 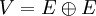 est muni de la forme symplectique
est muni de la forme symplectique  . Le graphe d'une application linéaire
. Le graphe d'une application linéaire  est un sous-espace lagrangien ssi T est symplectique.
est un sous-espace lagrangien ssi T est symplectique.Réduction symplectique
Si W est un sous-espace coisotropique de V, alors ω induit une forme symplectique sur l'espace quotient  .
.
 .
.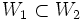 ssi
ssi  ;
; et
et  ;
; ;
; .
.